Literature Seminar:
Bridging Theory & Experiment with Metainference — a Bayesian Inference Approach
Robert M. Raddi
(Advisor: Dr. Vincent Voelz)
Tuesday, Nov 12th, 2019
4:00 pm in BE 162
Determining biological structures requires a combination of experiment and theory
Solving structures with NMR:
Experimental

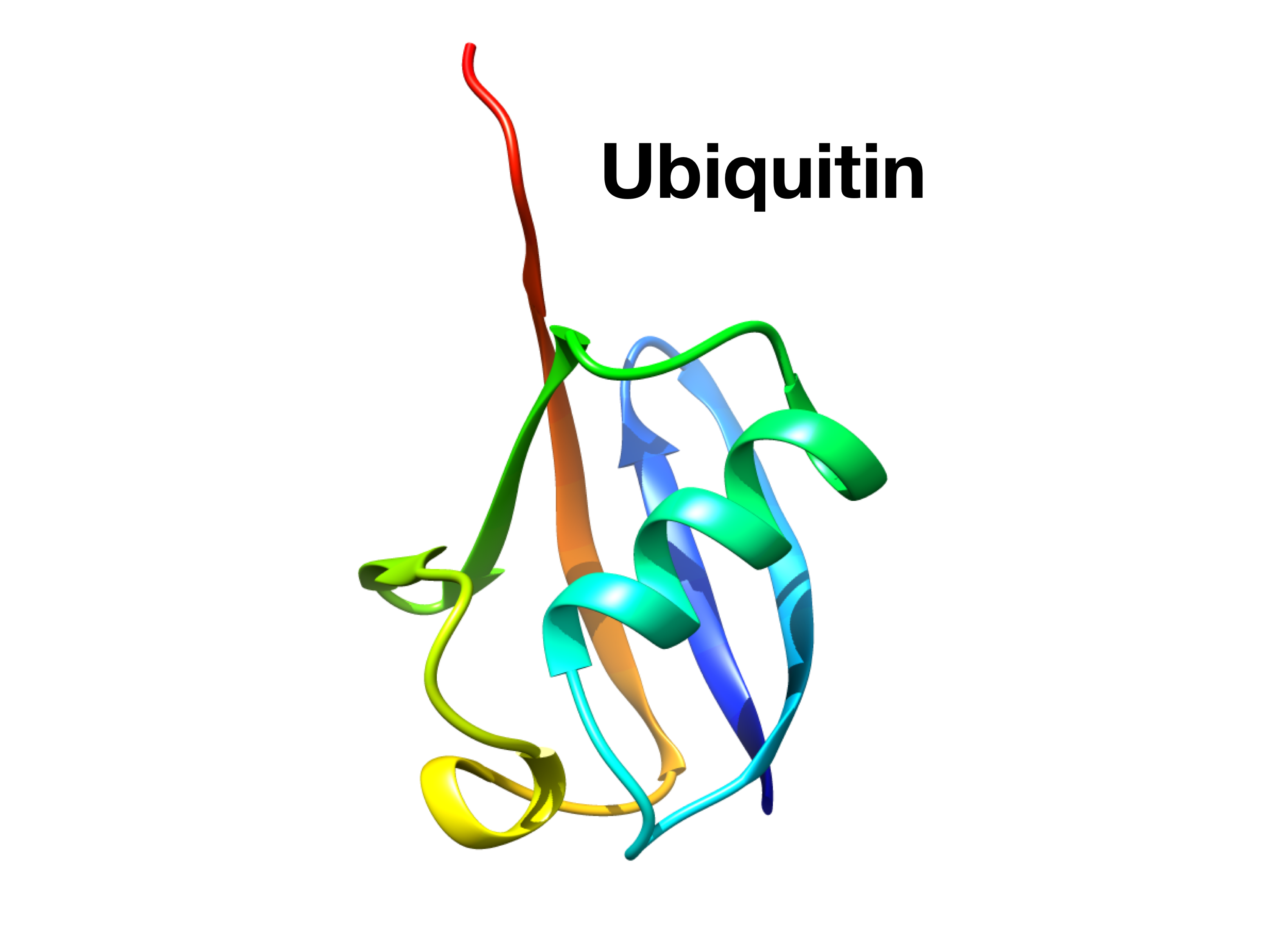
Computational:
References

Bayesian inference is the logical framework for combining separate sources of information
Laws of conditional probability
Combination of events:
The joint probability of some conformation $X$ and experimental data $D$ is $P(X,D) = P(X)P(D)$, where $X$ and $D$ are independent.
Conditional Probability:
Suppose we want to know how the outcome of some conformation $X$ is influenced by some experimental data $D$. Now the probability of some conformation $X$ and experimental data $D$ is
\begin{align} P(X, D) &= P(X|D)P(D)\\ \end{align}
\begin{align} \hspace{1.7cm}&= P(D|X)P(X) \end{align}
Bayes' Theorem:
$$P(X | D) = \space\space\frac{P(D|X)P(X)}{P(D)}$$
Bayesian inference of structured ensembles
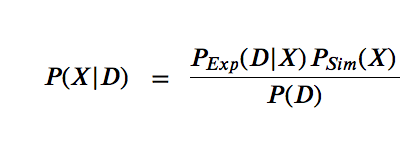
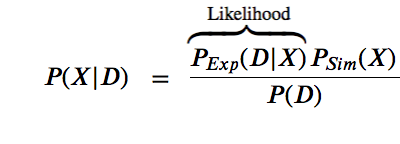
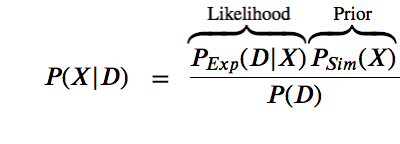
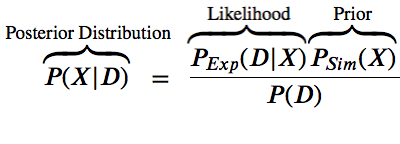
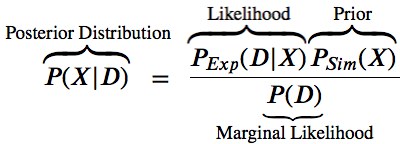
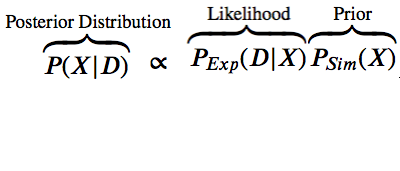
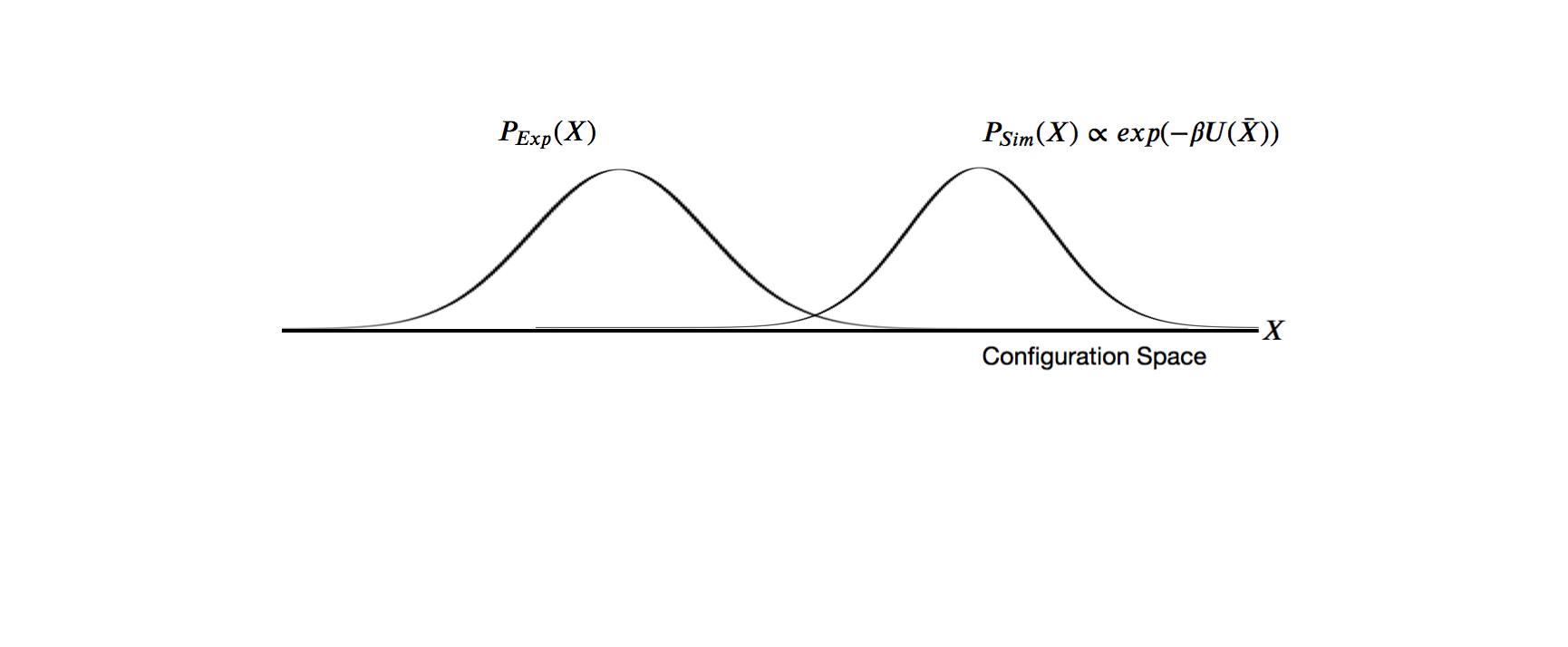
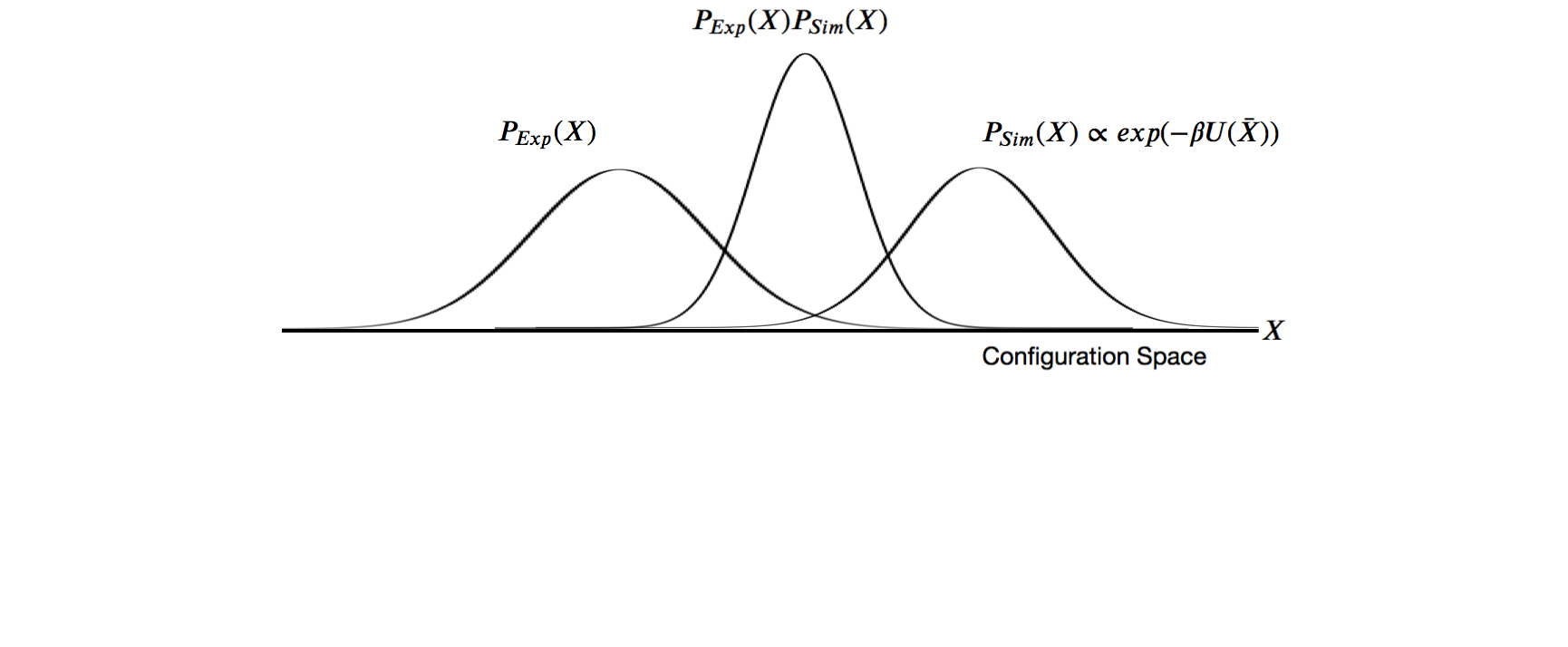
The likelihood function $P(D | X)$ is related to the experimental restraints (how well does X agree with D)
The prior $P(X)$ is the estimate of the probability before the data.
The posterior probability $P(X | D)$ is a function of some hypothesis (what we want to know).
$P(D)$ is the marginal likelihood is the same for all possible hypotheses. We treat as a normalization factor.
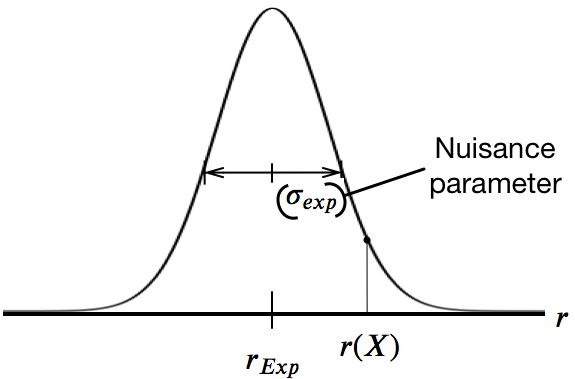
Incorporating errors:
Nuisance parameter $\sigma$, which could be chemical shifts, NOE distances, etc...
$\overbrace{P(X, \sigma | D)}^{\text{Posterior Distribution}} \propto \overbrace{P_{Exp}(D | X, \sigma)}^{\text{Likelihood}} \overbrace{P_{Sim}(X)}^{\text{Prior}} \overbrace{P(\sigma)}^{\text{Nuisance}\\\text{Parameter}}$
...this is how we make inferences in the face of uncertainty...
Posterior distribution can be sampled by Markov Chain Monte Carlo (MCMC)
Protocol for MCMC:
1. Start at some point $X$, $\sigma$. Compute $P(X,\sigma)$.
2. Roll dice and draw a new point $X^{*}$, $\sigma^{*}$. Compute $P(X^{*},\sigma^{*})$.
3. Accept move with probability $P_{accept}$ if: $$P_{accept} = min(1, \frac{P(X^{*},\sigma^{*})}{P(X,\sigma)}),$$ then set $X$, $\sigma$ = $X^{*}$, $\sigma^{*}$.
Ensemble of replicas of the system solves the problem of ensemble averaged data
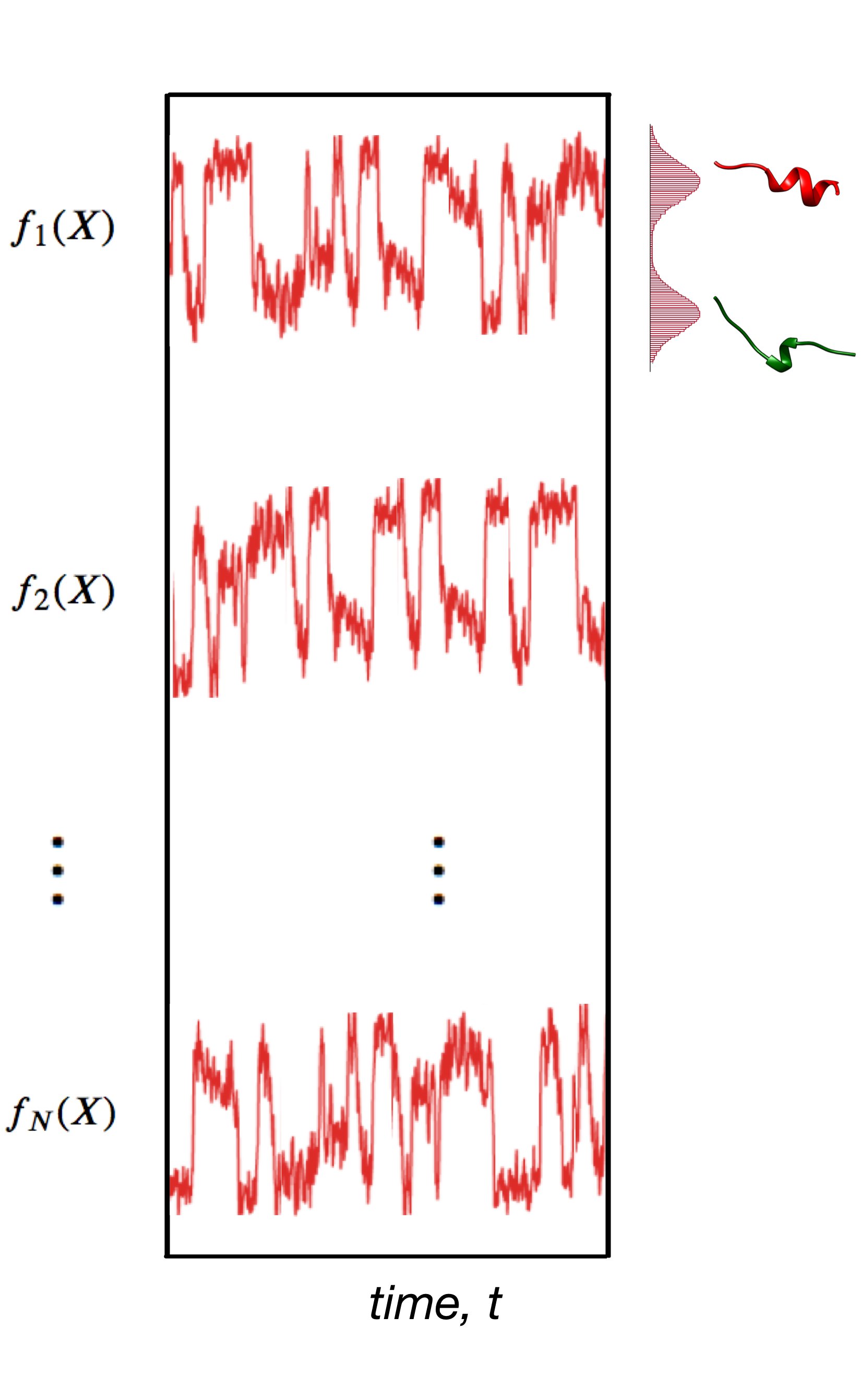
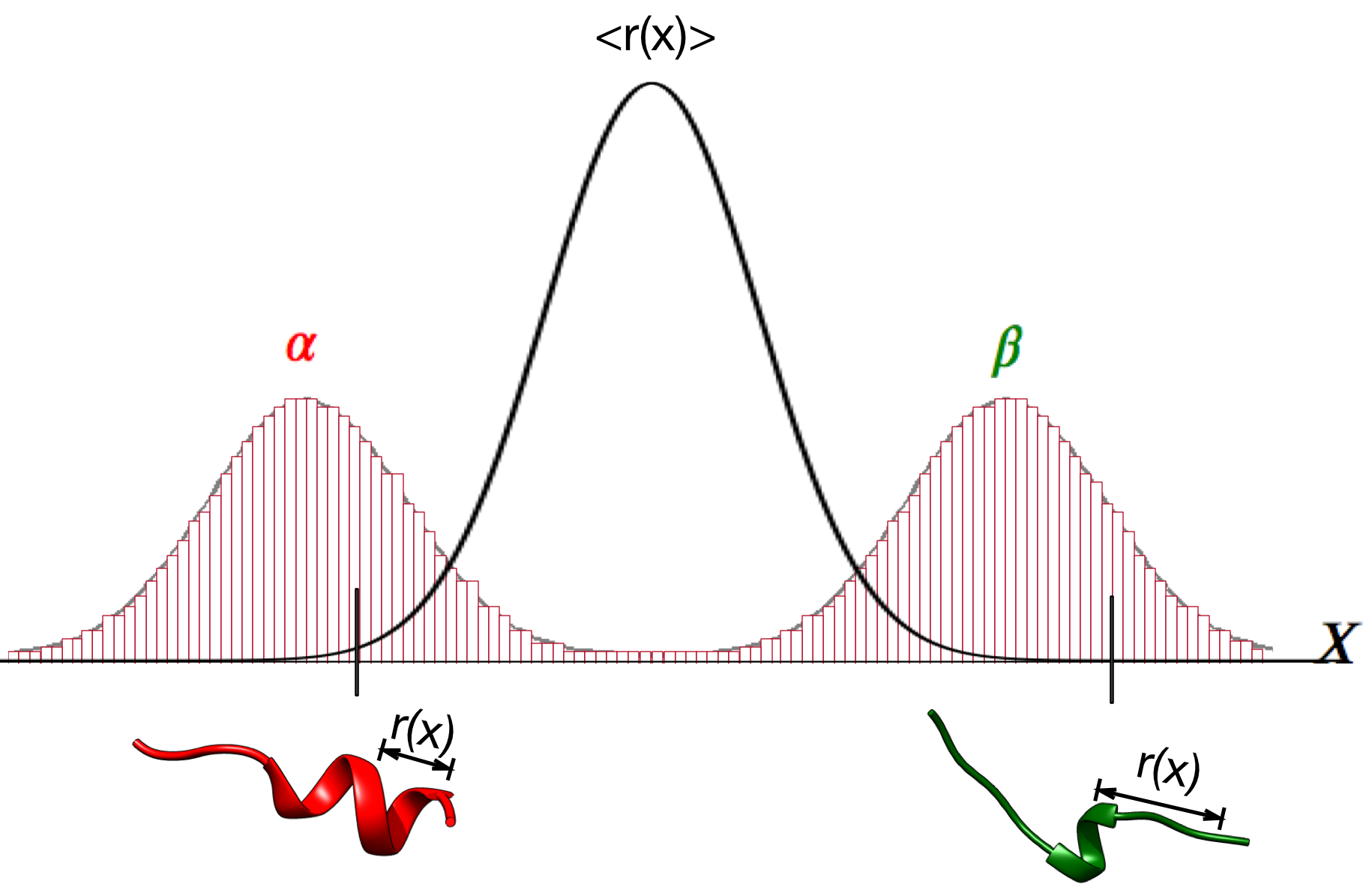
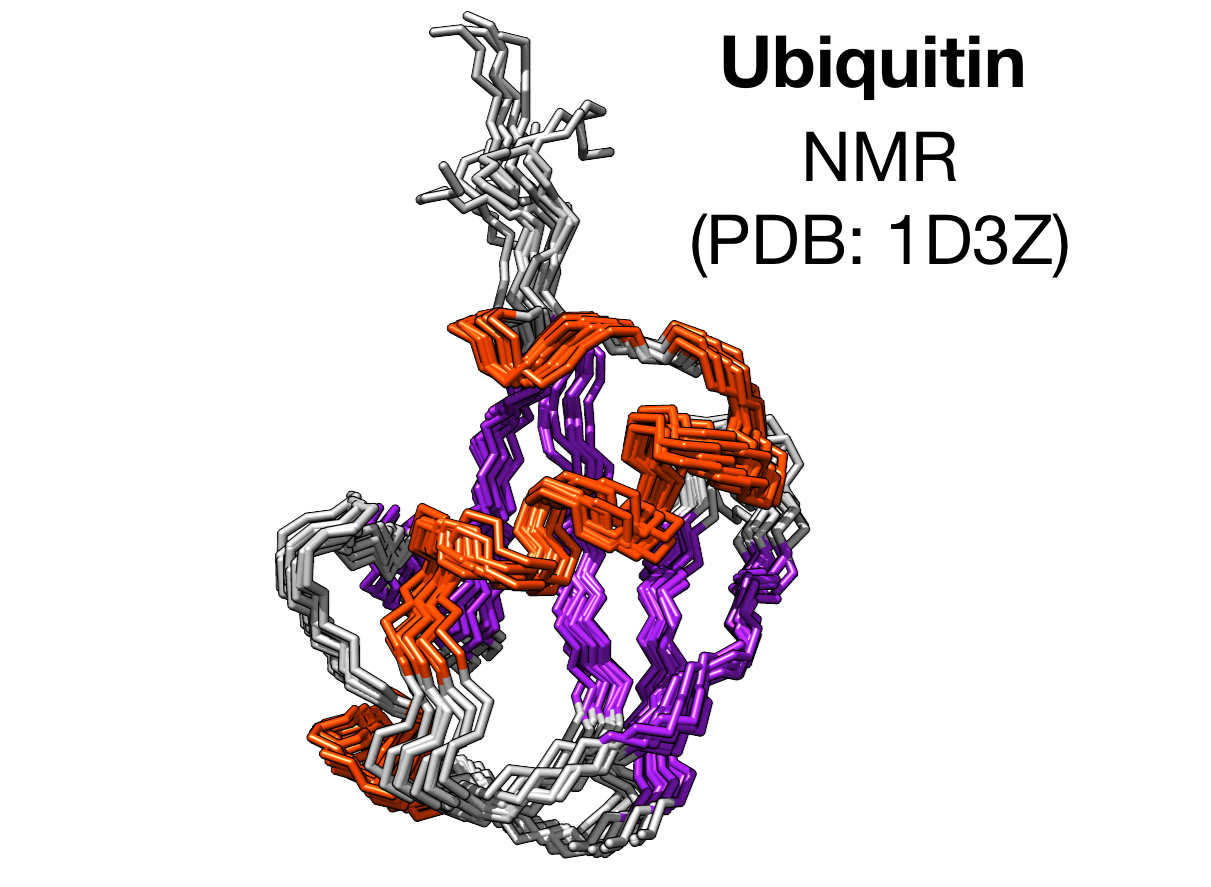
Testing Metainference with a well defined system—Ubiquitin
Ubiquitin — NMR structure (PDB: 1D3Z)
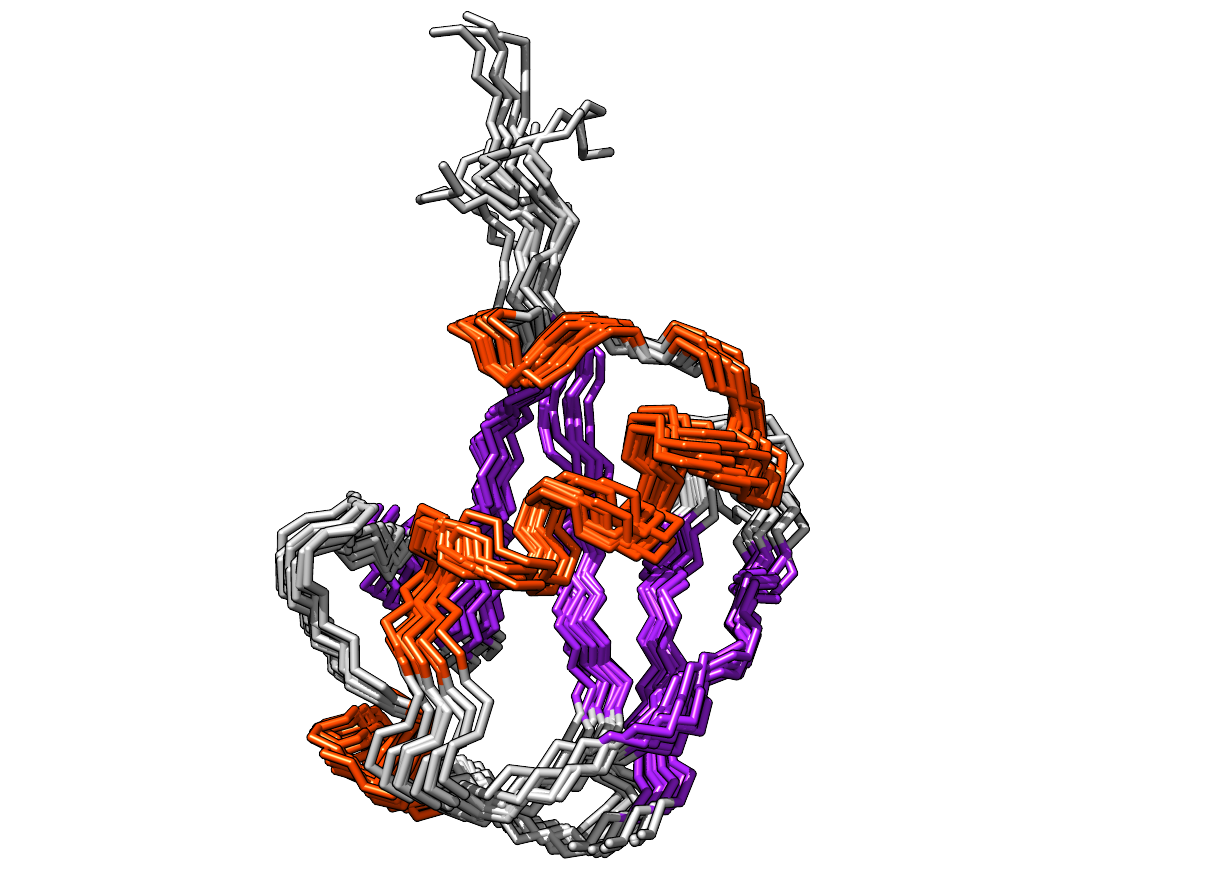
Modeling:
- Chemical Shifts: CA, CB, CO, HA, HN, NH
- RDC (set 1): NH, CAC, CAHA, CN, CH
Validation: (back-calculation of the Exp. data not used in modeling)
- Scalar Coupling: $^{3}J_{HNC}$, $^{3}J_{HNHA}$
- RDC (set 2): NH
- RDC (set 3): NH, CAC, CAHA, CN, CH
The Metainference ensemble supports previous findings
A known source of dynamics involves a flip of the backbone consisting of Aspartic acid—D52 and Glycine—G53.
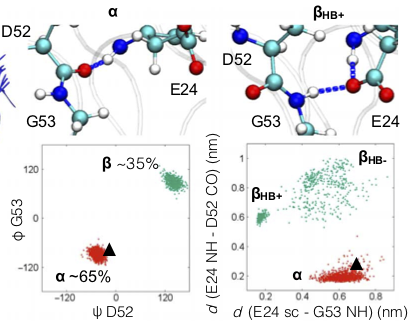
The flip is coupled with the formation of a H-bond ($\beta$ state) between the backbone of Glycine—G53 and side chain of Glutamic acid—E24
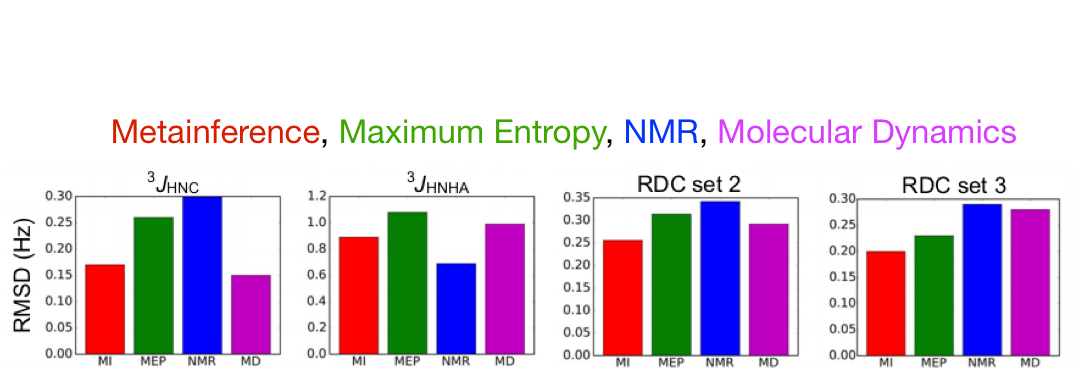
Validation
Summary
- Metainference algorithm combines experimental and theoretical models to infer conformational ensembles
- Bayesian inference is used for combining all sources of information to deal with uncertainty
- MI was applied to a classic system & method validation supports MI
Future directions
- Bayesian inference can be used to improve force fields in MD simulations
- Metadynamic Metainference - time-dependent bias potential acting on selected CVs
Thank You for listening : )
Voelz Lab — Halloween 2019
From left to right: Shahlo Solieva, Si Zhang, Vincent Voelz, Tim Marshall,
Steven Goold, Yunhui Ge, Robert Raddi, Dylan Novack, Matthew Hurley,
Lei Qian

Additional thanks to:
Dr. Wunder & classmates
