Reviewing: Intramolecular long-distance electron transfer in organic molecules
April 29th, 2019
by Robert M. Raddi
$\renewcommand{\hat}[1]{\widehat{#1}}$
History:¶
1924 —$Br\ddot{o}nsted$ Relationship¶
• Observations suggest a linear relationship between the reaction $E_{a}$ and the free energy $\Delta G$ of acid dissociation.
1956 & 1959 — Marcus¶
• Marcus replaces $E_{a} = a \Delta G + b$ with a parabola, $ E_{AB}(r) = m_{1} (r- r_{1})^{2} + b $
...Other works...¶
1986 & 1998 Closs (this author)¶
1992 — Marcus was awarded the Nobel Prize in Chemistry.¶
Motivation/Goal:¶
Develop experiments to prove Marcus theory & provide the necessary constants for predicting ET rates from simple structural parameters.¶
• From this work, designs of efficient photochemical charge-separation devices can be made.¶
Why have earlier attempts to verify Marcus' prediction of an inverted region failed?¶
• These tests were performed on intermolecular ET reactions, which, in comparison with intramolecular processes, include the additional step of bringing the reactants together by diffusion (rate limiting — producing a flat region on the $k_{ET}$ versus $\Delta G°$ curve)¶
Theory¶
Without eigenstates of mixing, followed in nonadiabatic reaction
Mixing of eigenstates followed by adiabatic reactions.
Arrhenius equation¶
$$k=A \exp \left[-E_{\mathrm{a}} / k_{\mathrm{B}} T\right]\label{eq:3}\tag{3}$$In Eyring's transition state theory (TST), the preexponential term, $A$ is replaced with $\kappa k_{B}T/h$, where $\kappa$ is the transmission coefficient.
The activation energy $E_{a}$ is replaced with $\Delta G^{\dagger}$.
Fermi's Golden Rule¶
Treat ET as radiationless transitions Rate constant can be separated into electronic, $|V|^{2}$ and nuclear coordinates, Franck-Condon-weighted density of states, $FCWD$.
$$k= \frac{2 \pi}{ \hbar}|V|^{2} (F C W D)\label{eq:5}\tag{5}$$The coupling matrix elements, V represents the resonance energy associated with the structures of reactant and product and can be directly obtained from MO theory.
Frank-Condon-weighted density of states (FCWD) must account for for the exponential dependence associated with the activation energy and temperature of equation $\ref{eq:3}$
Arrhenius equation connected with Marcus Theory¶
$$k_{\mathrm{ET}}=A^{\prime} \exp \left[-\left(\Delta G°+\lambda_{\mathrm{S}}\right)^{2}/4 \lambda_{\mathrm{S}} k_{\mathrm{B}} T \right]\label{eq:7}\tag{7}$$ $$k_{\mathrm{ET}}=\left(\pi / \hbar^{2} \lambda_{\mathrm{S}} k_{\mathrm{B}} T\right)^{1 / 2}|V|^{2} \exp \left(-G^{\dagger} / k_{\mathrm{B}} T\right)\label{eq:8}\tag{8}$$Arrhenius equation connected with Marcus Theory including the Franck-Condon-weighted density of states (FCWD)¶
$$k=\left(\pi / \hbar^{2} \lambda_{\mathrm{S}} k_{\mathrm{B}} T\right)^{1 / 2}|V|^{2} \sum_{w=0}^{\infty}\left(e^{-s} S^{w} / w !\right) \exp \left\{-\left[\left(\lambda_{\mathrm{S}}+\Delta G°+w h v\right)^{2} / 4 \lambda_{\mathrm{S}} k_{\mathrm{B}} T\right]\right\}\label{eq:9}\tag{9}$$¶
$$S=\lambda_{\mathrm{v}} / h v$$¶
$$\lambda_{\mathrm{s}}=e^{2}\left[\left(2 \mathrm{r}_{\mathrm{D}}\right)^{-1}+\left(2 r_{\mathrm{A}}\right)^{-1}-\left(R_{\mathrm{DA}}\right)^{-1}\right]\left(\epsilon_{\mathrm{S}}^{-1}+\epsilon_{\mathrm{op}}^{-1}\right)\label{eq:10}\tag{10}$$¶
Part 1: Experiments on ET Rates as a function of free energy and reorganization energy¶
$\mathrm{A} = \text{acceptor}$
$\mathrm{D} = \text{donor} \hspace{1cm};\hspace{1cm} \mathrm{D}^{*} = \text{excited donor state}$
$\mathrm{Sp} = \text{inert rigid spacer}\hspace{1.25cm} \text{e.g., Androstane (steroid spacer)}$
Charge separation from an excited donor state:¶
$$\mathrm{A}—\mathrm{Sp}—\mathrm{D}^{*} \longrightarrow \mathrm{A}^{-}—\mathrm{Sp}—\mathrm{D}^{+} \label{eq:1}\tag{1}$$Charge-shift reaction¶
$$\mathrm{A}—\mathrm{Sp}—\mathrm{D}^{-} \longrightarrow {\mathrm{A}^{-}}—{\mathrm{Sp}}—{\mathrm{D}} \label{eq:2}\tag{2}$$where the electronic interactions between D and A in equations $\ref{eq:1}$ and $\ref{eq:2}$ are extremely weak (<< 1 kcal).
Photoinduced Charge Separation¶
$$\overset{{D^{*} A_{1}, A_{2}}}{\underset{D, A_{1}, A_{2}}{\uparrow h\nu}} {}^{\searrow}_{\swarrow} {D^{+}, A_{1}^{-}, A_{2} \rightarrow D^{+}, A_{1}, A_{2}^{-}}\label{eq:11}\tag{11}$$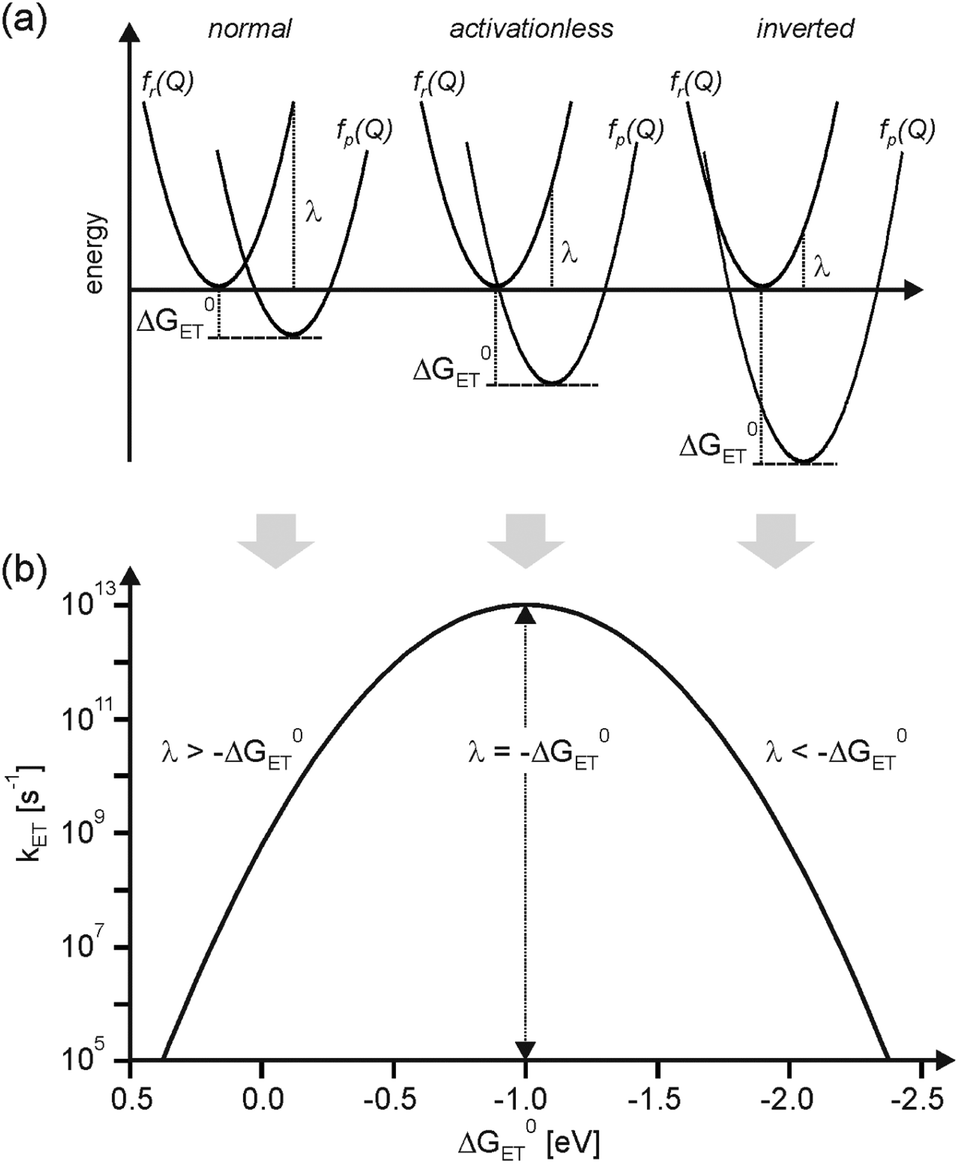
The maximum rate occurs when the free energy change of the reaction equals the sum of the solvent and vibrational reorganization energies.¶
Decreasing polarity of the solvent, the maximum rate should occur at a less negative free energy of the reaction.¶
Polarity: MTHF > di-n-butylether > isooctane¶
So, switching to less polar solvents causes the rates to increase drastically in these exoergic reactions, but also retards the rates of the reactions with large driving force.¶
Activationless electron transfer; Slightly Inverted; Largely Inverted¶
Part 2: Distance and Stereochemical Dependence of intramolecular ET Rates¶
How do rates respond to distance between donor and acceptor?¶
Distance Dependence of Intramolecular ET Rates¶
assumes an exponential decay of the wave function and the coupling matrix element, $V$ and $V_{0}$.
$$V=V_{0} \exp \left[-\beta\left(R-R_{0}\right) / 2\right]\label{eq:13}\tag{13}$$van der Waals separation, $R_{0}$, where $\beta$ is a constant scaling the distance dependence.
$$k=k_{0} \exp \left[-\beta\left(R-R_{0}\right)\right]\label{eq:14}\tag{14}$$Coupling comes from a pathway involving intervening bonds of the spacer.
Exponential decay of the wavefunction and coupling with respect to the # of spacer carbon atoms¶
$$V=V_{0}^{\prime} \exp \left[-\beta^{\prime}(N-1) / 2\right],\label{eq:15}\tag{15}$$where $R = R_{D}+R_{A}$. Also note that this equation only holds for linear molecules.
Please note that eq's $\ref{eq:13}, \ref{eq:14}, \ref{eq:15}$ do not include any terms regarding stereochemistry.¶