Table of Contents:¶
| Experiment # | Topic |
|---|---|
| 1. | A Colorimetric Determination of Aspirin in Commerical Preparations |
| 2. | Measuring the Vapor Pressure of a Volatile Liquid |
| 3. | Determination of Molar Mass by Freezing Point Depressions |
| 4. | Determination of a Rate Law |
| 5. | Determination of Activation Energy |
| 6. | Equilibrium and LeChatelierʹs Principle |
| 7. | Acids, Bases, Salts and Buffer Solutions |
| 8. | Acid Base Titration Curves I |
| 9. | Acid Base Titration Curves II |
| 10. | Gibbs Free Energy of a Dissolution Reaction |
| 11. | Electrochemical Cells |
| 12. | Written Lab Exam |
1.¶
Experiment #1 A Colorimetric Determination of Aspirin in Commercial Preparations ¶
WHY?¶
This lab was designed to help students develop the skills for determining the amount of a substance inside another substance by linear regression, where the equation of a line is given by Beer's Law.

In Nature: Voodoo Lilly:¶
Acetylsalicylic acid (main component of Asprin) is actually derived from the Voodoo Lilly. Salicylic acid is a plant hormone that triggers the Voodoo Lilly to emit a foul odor that attracts flies. The fly gets trapped inside the flower for a full day. During this time, the fly gets covered in pollen. The next morning it is released, where it then goes to another Voodoo Lilly to deposit the pollen.
- Analgesic properties were discovered at Baeyer in 1897. Acetylsalicylic acid works by inhibiting production of an enzyme—prostaglandin cyclooxygenase. (Note: Prostaglandins help transmit pain signals across synapses.)
Theory:¶

Derivation of Beer's Law:¶
Here is an image of the situation we wish to model:

The density of particles, $\rho$ and the absorption coefficient, $\alpha$ multiplied by the intensity, I shown in the 1st order differential equation: $$ -\frac{\partial{I}}{\partial{x}} = I \alpha \rho $$
Combine like-terms to each side of the equation:
$$\int_{I_{0}}^{I} \frac{\partial{I}}{I} = -\int_{0}^{x} \alpha \rho \partial{x} $$We know that $\int \frac{1}{x}dx = ln(x)$, so
$$ln(\frac{I}{I_{0}}) = - \alpha \rho x, $$To get the general solution of the D.E we can take the exponential of both sides
$$\frac{I}{I_{0}} = e^{-\alpha \rho x} $$General Solution to the D.E:
$$I (x) = I_{0} e^{-\alpha \rho x}$$Otherwise, to continue deriving Beer's Law we can use the property of logarithms:
$$-ln(\frac{I}{I_{0}}) = ln(\frac{I_{0}}{I}) = \alpha \rho x, $$and since we know the following
$$log_{10}(x) = \frac{ln(x)}{ln(10)},$$then we can say
$$ log_{10}(\frac{I_{0}}{I}) = \frac{\alpha \rho x}{ln(10)}$$Finally, we can say that $\rho \propto c$. We can also simplify further by saying $\epsilon =\frac{\alpha}{ln(10)}$, which has units of $M^{-1}cm^{-1}$ and $x = b$, where b is in cm.
$$ A = ln(\frac{I_{0}}{I}) = \epsilon b c$$Theory - a brief Introduction to Quantum Mechanics - particle in a box (PIB)¶
$$\Delta E = E_{S_{1}} − E_{S_{0}}$$$$E_{n} =\frac{h^{2}n^{2}}{8ma^{2}}$$$$ \Delta E = \frac{h^{2}(N+1)^{2}}{8ma^{2}} = h\nu = \lambda $$n = 1, 2, 3..., h = 6.62608 × 10-34 J·s (Planck’s constant), m = 9.10939 × 10-31 kg (mass of an electron), and a = length of the box (in meters if using SI units).
Solving for the box length, a, gives:
$$a = \sqrt{\frac{h\lambda (N+1)}{8mc} } $$The box length, a, may also be related to the polyene structure with the empirical formula:
$$a = (P · l) + E$$where $P$ is the number of C atoms in the conjugated chain, $l$ is the C-C bond length in the chain, and $E$ is the effective size of the end-groups.
Where & how can this be applied?¶
$\beta$-carotin is the chemical that gives carrots their characteristic orange color. Absorbance is around 450 nm (violet-blue), so we see orange, which is the light transmitted.
Color Wheel with corresponding wavelengths:¶

In this experiment, you will use a colorimeter to measure the absorbance of tetraaqua salicylate iron(III) complex.¶
_complex.png)
Jump to table of contents.¶
Post-Lab Questions:¶
- Using your data show the calculation of the concentration of acetylsalicylic (ASA) in Solution S
- Using your data show the calculation of the concentration of the iron tetraaquasalicylato ion, [Fe(H2O)4SA+ in Solution 1
- Include your excel graph of the Beer’s Law plot witht his addendum. The trendline and its equation must be displayed. Be sure the equation of the trendline has 6 significant digits for the slope and intercept (by using “format trendline”)
- Using your data show the calculation of the the concentration of the acetylsalicylic acid solution in the 50.00 mL sample (part B of experiment)
- Using your data show the calculation of the concentration of the acetylsalicylic acid solution in the 2.00 mL aliquot (part B of experiment). This value also equal the concentration in the 250 mL volumetric flask containing the dissolved aspirin.
- Using your data show the calculation of the mass (in mg) of acetylsalicylic acid in the tablet:
List three possible experimental errors that may have caused deviation of your answer to 6 from the accepted value. For each error, indicate whether you expect the error would cause your calculated value of the mass to be larger or smaller than the correct value.
I) If the colorimerter was not properly calibrated, or the cuvette was not properly rinsed for each run. This can cause a deviation in the Absorbance measurement. II) If the NaOH/dissolved tablet solution was transfered when it was still very hot, then there exists a higher probability that the tablet filler seeped through the filter during gravity filtration. If this was the case, then the mass of the acetylsalicylic acid would be greater than that of the mass of acetylsalicylic acid that appears on label. III) If students recorded the mean absorbance at one instance (not selecting all data for that run), then the $A_{mean}$ would not represent the true value.
Jump to table of contents.¶
2.¶
Experiment #2 Measuring the Vapor Pressure of a Volatile Liquid ¶
WHY?¶
The purpose of this lab is to investigate the temperature dependence of vapor pressure for a volatile liquid.
Theory:¶
General form of the Clausius-Clapeyron equation¶
$$\frac{dP}{dT}=\frac{\Delta \bar{H}}{T\Delta \bar{V}}=\frac{\Delta \bar{H}}{T}\frac{1}{(\bar{V}_{gas}−\bar{V}_{liquid})}$$We can assume that the volume of the gas is much larger than the volume of the liquid. $$\bar{V}_{gas} >> \bar{V}_{liquid},$$
which means that $\bar{V}_{liquid} \rightarrow 0$. Suppose the vapor is an ideal gas, then
$$\bar{V}_{gas}=\frac{RT}{P}$$Plugging this equation into the right side of the general form of the Clausius-Clapeyron equation gives
$$\frac{\Delta \bar{H}_{vap}}{RT^{2}} = \frac{1}{P}\frac{dP}{dT} = \frac{dln(P)}{dT}$$To obtain the general expression for pressure, we can use separation of variables and integrate both sides.
$$\int dln(P)=\int \frac{\Delta \bar{H}_{vap}}{RT^{2}}dT$$$$ln(P)= -\frac{\Delta \bar{H}_{vap}}{RT}$$Then, we can take the exponential of both sides to cancel out the natural log to obtain:
$$P \propto e^{-\Delta H_{vap}/RT} $$¶
To obtain a more useful form of the Clausius-Clapeyron equation we can integrate both sides with limits from $T_{1}$ to $T_{2}$ and $P_{1}$ to $P_{2}$:
$$\int_{P_{1}}^{P_{2}} dln(P)=\int_{T_{1}}^{T_{2}} \frac{\Delta \bar{H}_{vap}}{RT^{2}}dT$$Clausius-Clapeyron equation¶
$$ln(\frac{p_{2}}{p_{1}})=-\frac{\Delta H_{vap}}{R}(\frac{1}{T_{2}}-\frac{1}{T_{1}}) $$In this experiment, we will break down the Clausius-Clapeyron equation into parts. First we need to use the proportionality equation $P_{1}T_{2} = P_{2}T_{1}$, which assumes there is no change in volume $V_{1} = V_{2}$. We can rearrange and say that $P_{1} = P_{air}$ and $P_{2} = P_{airRT}$ in kPa. $T_{1} = T_{surr}$, which is the temperature of the water in the flask surrounding the Erlenmeyer flask.
$$P_{air} = P_{airRT}(\frac{T_{sys}}{T_{surr}}),$$where temperature has units of Kelvin. We want to find $\Delta H_{vap}$, which has units of kJ $mol^{-1}$ and can be found by plotting the Clausius-Clapeyron equation and extracting the slope of the line $ y = mx + b$.
$$ ln(P_{vap}) = -\frac{\Delta H_{vap}}{R}\frac{1}{T} + ln{\beta},$$where $P_{vap} = P_{total} - P_{air}$ and $P_{total} = P_{airRT} + P_{vapTheo.}$. The slope, m is $-\frac{\Delta H_{vap}}{R}$, so
$$-\Delta H_{vap} = mR$$EXAMPLE: Boiling water at high altitudes.¶
Water boils at $T_{1}$ = 373 K and $p_{1}$ = 1 atm. At a high altitude where $p_{2}$ = 0.5 atm, what is the boiling temperature $T_{2}$? The enthalpy of vaporization for water, is $\Delta H_{vap}$ = 40.66 kJ $mol^{−1}$.
Rearranging, and substituting the enthalpy of vaporization for water, $\Delta H_{vap}$ = 40.66 kJ $mol^{−1}$ into the Clausius-Clapeyron equation gives
$$ln(\frac{p_{2}}{p_{1}})=-\frac{\Delta H_{vap}}{R}(\frac{1}{T_{2}}-\frac{1}{T_{1}}) \implies \frac{1}{T_{2}}=\frac{1}{T_{2}}-\frac{R}{\Delta H_{vap}}ln(\frac{p_{2}}{p_{1}}) $$$$\frac{1}{T_{2}}=\frac{1}{373}-\frac{8.314 J K^{−1} mol^{−1}}{40,660 J mol^{-1}}ln(\frac{1}{2}) \implies T_{2} = 354 K = 81°C$$Therefore, water boils at lower temperatures at higher altitudes.
Trends: Normal boiling points¶
Consider the following:
Intermolecular forces: Ionic > Hydrogen > dipole-dipole > Van der waals
Number of carbon atoms along chain
Branching $\downarrow$ $B_{pt}$
Example: Rank the following molecules in order of boiling points:¶
Isopropanol ; Ethanol ; Methanol ; 3-pentanol ; pentanol
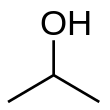




Pentanol (137°C) > 3-pentanol (115°C) > Isopropanol (82°C) > Ethanol (78°C) > Methanol (65°C)
Jump to table of contents.¶
3.¶
Experiment #3 Determination of Molar Mass by Freezing Point Depressions ¶
WHY?¶
This experiment explores the idea of freezing point depression, which has many applications e.g., dumping salt on the roadways (Salt in $H_{2}O$ [0°C $\rightarrow$ -21°C]). Students will also learn about Blagden's Law, the Cryoscopic constant ($K_{f}$), as well as determine the molecular weight of an unknown acid when creating a mixture of Lauric acid and the unknown acid via the freezing point.
If the solution is treated as an ideal solution, the extent of the freezing point depression depends only on the solute concentration. This is a simple linear relationship that is described by Blagden's Law. Sir Charles Blagden (1748-1820) who was an assistant to Cavendish (1731-1810) (discovered Hydorgen) found that the temperature of freezing point, $T_{f}$ is proportional to the product of the Cryoscopic constant, $K_{f}$ (depends only on the solvent), the molality, $m$ (mol of solute per kg of solvent) and the Van't Hoff factor, $i$ (# of ion particles per individual molecule of solute e.g., i = 2 for NaCl and i = 3 for $BaCl_{2}$).
$$\Delta T_{f} = T_{f}(Solv.) - T_{f}(Soln.) = K_{f} mi, \tag{1} $$where the melting point of solvent (lauric acid) is subtracted from the melting point of the solution (unknown with lauric acid).
Note: In this experiment, we will be omitting the Van't Hoff factor, $i$ because we are using solutes that are nonelectrolytes (i=1)¶
Why lauric acid?¶
 The melting point is relatively high, so we are able to study the freezing behavior at a convenient temperature.
Lauric acid, $C_{12}H_{24}O_{2}$ has a molecular weight of 200.322 g·$mol^{−1}$ and its melting point is 43.8 °C (110.8 °F; 316.9 K).
The melting point is relatively high, so we are able to study the freezing behavior at a convenient temperature.
Lauric acid, $C_{12}H_{24}O_{2}$ has a molecular weight of 200.322 g·$mol^{−1}$ and its melting point is 43.8 °C (110.8 °F; 316.9 K).
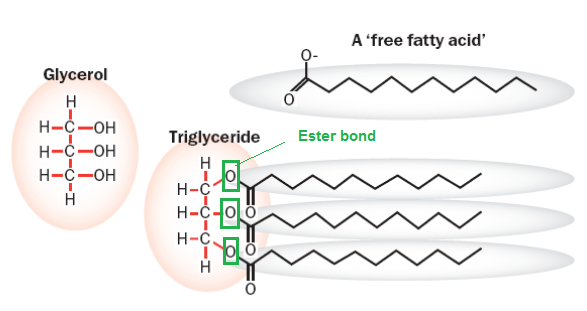
Coconut oil contains about 49%
Although 95% of medium-chain triglycerides are absorbed through the portal vein, only 25-30% of lauric acid is absorbed through it.
Saturated fatty acids¶
Butyric acid with 4 carbon atoms (contained in butter)
Lauric acid with 12 carbon atoms (contained in coconut oil, palm kernel oil, and breast milk)
Myristic acid with 14 carbon atoms (contained in cow's milk and dairy products)
Palmitic acid with 16 carbon atoms (contained in palm oil and meat)
Stearic acid with 18 carbon atoms (also contained in meat and cocoa butter)

Naphthalene ($C_{10}H_{8}$) has a molecular weight of 128.1705 g/mol and a melting point of 80.26°C.
Camphor ($C_{10}H_{16}O$) has two possible enantiomers (shown in the image below). Camphor has a molecular weight of 152.23 g/mol and a melting point of 175°C.

Calculations:¶
Let $m_{LA}$ be the mass of lauric acid and $m_{unknown}$ be the mass of the unknown.
It may be difficult to determine the exact freezing point due to the curvature of the Temperature Vs. Time plot during the transition from just before freezing to just after freezing. To circumvent this issue, we can take the slope of both portions and set them equal to each other to find the intersection of these lines.

The latter procedure is how we obtain $T_{f}(Soln.)$.
$$ T_{f}(Soln.) = \frac{m_{2}b_{1} - m_{2}b_{1}}{m_{2} - m_{1}} $$Then, we're able to determine the freezing point depression, $\Delta T_{f}$ by the following equation:
$$\Delta T_{f} = T_{f}(Solv.) - T_{f}(Soln.) = K_{f} mi, $$The molecular weight of the unknown is determined by
$$MW_{unknown} = \frac{m_{unknown} K_{f}(\text{lauric acid})}{m_{LA} \Delta T_{f}}$$¶
Jump to table of contents.¶
4.¶
Experiment #4 Determination of a Rate Law ¶
WHY?¶
This lab we will be learning about kinetics and reactions rates. We learn that the order of the reaction is not necessarily related to the stoichiometry of the reaction. It can be determined by experiment only. We achieve the latter using the initial rate method.
Not only do we determine reaction speeds from kinetics, but we can also determine reaction mechanism.
$$ H_{2}O_{2} (aq) + I^{-}\underset{k_{-1}}{\stackrel{k_{1}}{\rightleftharpoons}} 2H_{2}O (l) + O_{2} + I^{-} (aq) \tag{1}$$ $$ Rate = - \frac{1}{2}\frac{d [H_{2}O_{2}]}{dt} = -\frac{d[I^{-}]}{dt} = \frac{d[O_{2}]}{dt} $$
We will use potassium iodide ($KI$) to catalyze the decomposition, where the iodide ion ($I^{-}$) acts as the catalyst.
In this experiment, we will vary the concentration of the hydrogen peroxide while keeping the concentration of $KI$ the same.
Conversely, we will vary the concentration of the iodide ion while keeping the concentration of the hydrogen peroxide fixed.
You will need to determine the following:
The order of the reaction for hydrogen peroxide
The order of the reaction for iodide
The rate constant for the reaction
First, we take rearrange and take the log of both sides in order to linearize the equation. We do this to obtain an equation that will give us the slope equal to the order of reaction.
$$ Rate = k^{\prime} [H_{2}O_{2}]^{P}, $$where we let $k^{\prime} = k[I^{-}]^{q}$ because this is the species that we keep constant throughout the reaction. Then we continue to rearrange and solve.
$$ ln(\frac{Rate}{k^{\prime}}) = P ln([H_{2}O_{2}]) $$$$ ln(Rate) = P ln([H_{2}O_{2}]) + ln(k^{\prime})$$In the next part of the experiment, we will vary $[I^{-}]$ while keeping $[H_{2}O_{2}]$ constant. The previous mathematical procedure will be applied with the respective changes.
Lastly, we will determine the rate constant, k by rearranging and solving by plugging in our variables.
$$ Rate = k [H_{2}O_{2}]^{P}[I^{-}]^{q} $$$$ k = \frac{Rate}{[H_{2}O_{2}]^{P}[I^{-}]^{q}} $$5.¶
Experiment #5 Determination of Activation Energy ¶
WHY?¶
This experiment is to build on the last. The initial concentration of the reactants will be held constant and temperature will be varied. Here, we will explore the the effect of temperature on the reaction rate.
Crystal violet is a purple dye that slowly decolorizes when mixed with strong base. The rate of this process will be measured by monitoring absorbance using a colorimeter.
$$Rate = k^{\prime}[CV^{+}]^{P} ,\tag{1}$$where $k^{\prime} = k[OH^{-}]^{q}$ and $A=\epsilon b c$.
$$ Rate = -\frac{dA}{dt} = k^{\prime\prime} A^{P},\tag{2}$$where $k^{\prime\prime} = \frac{k^{\prime}}{(\epsilon b)^{P}} = \frac{k[OH^{-}]^{q}}{(\epsilon b)^{P}}$
The integrated rate law with have a different form determining the order of the reaction, $P$.
We need to rearrange equation 2 by getting like-variables to one side of the equation:
$$ \frac{dA}{A^{P}} = -k^{\prime\prime} {dt}$$For a 0th order integrated rate law: let p = 0
$$ \int_{A_{0}}^{A_{t}}\frac{dA}{A^{0}} = \int_{0}^{t} -k^{\prime\prime} {dt} \implies \int_{A_{0}}^{A_{t}}dA = \int_{0}^{t} -k^{\prime\prime} {dt}$$$$ A_{t}-A_{0} = -k^{\prime\prime}t $$$$ A_{t} = -k^{\prime\prime}t + A_{0} $$For a 1st order integrated rate law: let p = 1
$$ \int_{A_{0}}^{A_{t}}\frac{dA}{A^{1}} = \int_{0}^{t} -k^{\prime\prime} {dt} \implies \int_{A_{0}}^{A_{t}}\frac{1}{A}dA = \int_{0}^{t} -k^{\prime\prime} {dt}$$$$ ln(\frac{A_{t}}{A_{0}}) = ln(A_{t}) - ln(A_{0}) = -k^{\prime\prime}t $$$$ ln(A_{t}) = -k^{\prime\prime}t + ln(A_{0})$$For a 2nd order integrated rate law: let p = 2
$$ \int_{A_{0}}^{A_{t}}\frac{dA}{A^{2}} = \int_{0}^{t} -k^{\prime\prime} {dt} \implies \int_{A_{0}}^{A_{t}}\frac{1}{A}dA = \int_{0}^{t} -k^{\prime\prime} {dt}$$$$ (\frac{1}{A_{t}}-\frac{1}{A_{0}}) = -k^{\prime\prime}t $$$$ \frac{1}{A_{t}} = -k^{\prime\prime}t+\frac{1}{A_{0}}$$Theory¶
Concept of Activation Energy, $E_{a}$¶
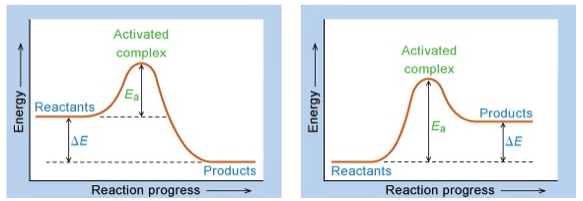
Temperature Dependence of Rate Constants¶
Arrhenius first proposed that the rate constant obeyed
$$ k = A e^{-\frac{E_{a}}{RT}}, $$¶
where A is a temperature independent factor proportional to the number of collisions per unit time. As previously stated, $E_{a}$ is the activation energy.
$$ ln(k) = ln(Ae^{-\frac{E_{a}}{RT}}) = ln(A) -\frac{E_{a}}{RT} \implies ln(k)=-\frac{E_{a}}{R}(\frac{1}{T}) + ln(A)$$¶
You might see in this form that the equation resembles a line:
$$ y = mx +b $$$$ ln(k)=-\frac{E_{a}}{R}(\frac{1}{T}) + ln(A)$$
Now, suppose that at two different temperatures T1 and T2, reaction rate constants k1 and k2.
$$ ln(k_{1})=-\frac{E_{a}}{R}(\frac{1}{T_{1}}) + ln(A)$$and
$$ ln(k_{2})=-\frac{E_{a}}{R}(\frac{1}{T_{2}}) + ln(A)$$Then,
$$ ln(\frac{k_{2}}{k_{1}})=-\frac{E_{a}}{R}(\frac{1}{T_{2}} - \frac{1}{T_{1}}) + ln(A)$$</h2>
Jump to table of contents.¶
6.¶
Experiment #6 Equilibrium and LeChatelierʹs Principle ¶
WHY?¶
This qualitative experiment will explore some of the key notions of equilibrium chemistry.
Theory¶
Equilibrium Chemistry¶
The Chemical potential, $\mu$ in a sense describes the movement or diffusion of material (concentration gradient) moving from high concentration to low concentration.
The chemical potential is sometimes referred to as the escaping tendency because the higher the value of $\mu$, the greater the tendency for particles in state $B$ to enter state $A$.
The chemical potential can be related to the change in Gibbs free energy, $\Delta G$
In this experiment we are strictly dealing with aqueous solutions, but what if we used gases? How would the change in pressure effect the shift in equilibrium?

What if you add a catalyst?
No difference!
EDTA - Ethylenediaminetetraacetic acid¶
hexadentate ligand and chelating agent agent
chelation therapy, such as for treating mercury and lead poisoning.
In part D of this experiment you will be studying the following reaction:¶
$$ Fe^{3+} (aq) + SCN^{-}(aq) \rightleftharpoons [FeSCN]^{2+}(aq)$$Suppose we were measuring the absorbance of $[FeSCN]^{2+}$ similar to experiment #1 (A Colorimetric Determination of Aspirin in Commerical Preparations). As we know, Beer's law ($A=\epsilon bc$) relates absorbance, A with the concentration of a certain species, c. Let us now consider the goal of determining the concentration of the reactants at equilibrium.
| ————— | ——— $Fe^{3+} (aq)$ ——— | ——— $SCN^{-}(aq)$ ——— | ——— $[FeSCN]^{2+}(aq)$ ——— |
|---|---|---|---|
| I | $[Fe^{3+}]_{0}$ | $[SCN]_{0}$ | 0 |
| C | $-x$ | $-x$ | $+x$ |
| E | $[Fe^{3+}]_{0}-x$ | $[SCN]_{0}-x$ | $x=[FeSCN]^{2+}$ |
Then, the concentrations of our reactants at equilibrium are:
$$[Fe^{3+}]_{eq} = [Fe^{3+}]_{0}-x = [Fe^{3+}]_{0}-[FeSCN]^{2+} $$$$[SCN]_{eq} = [SCN]_{0}-x = [SCN]_{0}-[FeSCN]^{2+}$$Then solving for $K_{eq}$ gives
$$ K_{eq} = \frac{[FeSCN]^{2+}}{[Fe^{3+}][SCN^{-}]} = \frac{([FeSCN]^{2+})}{([Fe^{3+}]_{0}-[FeSCN]^{2+} )([SCN]_{0}-[FeSCN]^{2+})} = \frac{[FeSCN]^{2+}}{[FeSCN]^{2+}([Fe^{3+}]_{0}-1 )([SCN]_{0}-1)}$$$$ K_{eq} = \frac{1}{([Fe^{3+}]_{0}-1 )([SCN]_{0}-1)}$$Jump to table of contents.¶
7.¶
Experiment #7 Acids, Bases, Salts and Buffer Solutions ¶
WHY?¶
This experiment
Theory¶
pH, pKa, Buffers, and the Henderson-Hasselbach Equation¶
pH¶
- What is pH? How is it obtained?
$Nernst$ equation
$$E=E^{0}+{\frac{RT}{nF}}{ln(Q)} ,$$where F is Faraday's constant and Q is the reaction quotient. Recall that as the system goes to equilibrium, $Q \rightarrow K_{eq}$. Faraday's constant is defined as $F= e N_{A} = 96485.3 C mol^{−1}$, where $N_{A}$ is Avogadro's number and the charge of an electron, $e$ is $1.602×10^{−19} C$.
$$ Q = \frac{[FeSCN]^{2+}}{[Fe^{3+}][SCN^{-}]} $$$${\displaystyle E=E^{0}+{\frac {2.303RT}{F}}{\text{pH}}}$$Strong Acids and Strong Bases¶
$$K_{a}K_{b} = K_{w} = 1.0\times10^{-14} \hspace{1cm}(\text{at 25°C})$$When $K_{a} > K{b}$, solution is acidic.
When $K_{a} < K{b}$, solution is basic.
pKa¶
$pKa = - log_{10}(Ka)$
Buffers¶
Buffers are solutions that resists a change in pH.
$Henderson-Hasselbach$ equation¶
The $Henderson-Hasselbach$ equation is used when calculating the pH of buffer solution. Let's derive this expression now.
Suppose we have the general chemical equation for an acid undergoing hydrolysis.
$$ HA + H_{2}O \rightleftharpoons H_{3}O^{+} + A^{-} \hspace{1.5cm} K_{a} =\frac{[H_{3}O^{+}][A^{-}]}{[HA]}$$We can rearrange the acid dissociation
$$ [H_{3}O^{+}] = Ka \frac{[HA]}{[A^{-}]}= Ka \frac{[Acid]}{[Base]},$$where $[H_{3}O^{+}] = 10^{-pH}$ and we know from the laws of logarithms that $log_{10}(10^{-pH}) = -pH$.
$$ - log_{10}(10^{-pH}) = pH = - log_{10}(Ka \frac{[HA]}{[A^{-}]}) = - log_{10}(Ka) - log_{10}(\frac{[HA]}{[A^{-}]}), $$where we also know that the $pKa$ is defined as $pKa = - log_{10}(Ka)$.
$$ pH = pKa - log_{10}(\frac{[HA]}{[A^{-}]})$$If we remove the negative sign before the log, then we have to take the inverse of whatever is being operated on, which gives the most common form of the $Henderson-Hasselbach$ equation.
$$ pH = pKa + log_{10}(\frac{[A^{-}]}{[HA]})$$Jump to table of contents.¶
8.¶
Experiment #8 Acid Base Titration Curves I ¶
WHY?¶
See the lab manual for abstract and theory
Calculating the concentration of KHP¶
$$ M_{1} V_{1} = M_{2} V_{2} $$$$ \frac{mass_{KHP}MW_{KHP}}{V_{1}}V_{1} = M_{2} V_{2} \implies M_{2} = \frac{mass_{KHP}MW_{KHP}}{V_{2}} ,$$where $V_{2}$ is the volume of NaOH dispensed inside the beaker of KHP with 50 mL of solvent.
Why are we using KHP?
KHP (Potassium hydrogen phthalate) $\mathrm{C}_{8} \mathrm{H}_{5} \mathrm{KO}_{4}$ is a monobasic acid with a high molecular weight ($204.222 \mathrm{g} \cdot \mathrm{mol}^{-1}$) that can be highly purified, and does not readily reaction with the atmosphere. Therefore, it can maintain a constant weight more easily and be used as a primary standard knowing that we will obtain a very accurately-measured mass.
$$\mathrm{HP}^{-}+\mathrm{H}_{2} \mathrm{O} \rightleftharpoons \mathrm{P}^{2-}+\mathrm{H}_{3} \mathrm{O}^{+}$$KHP is mainly used for standardization of aqueous base and perchloric acid in acetic acid solutions. Some alternatives we can use in the lab as primary standards are: potassium permanganate ($KMnO_{4}$) and potassium hydroxide ($KOH$). Sodium carbonate ($Na_{2}CO_{3}$) is used for standardization of hydrochloric acid ($HCl$), sulfuric acid ($H_{2}SO_{4}$) and other aqueous acids, but not including acetic acid. Also, potassium bromate ($KBrO_{3}$) can be used for standardization of various sodium thiosulfate solutions.
$$K_{\mathrm{a}}=\frac{[\mathrm{B}]\left[\mathrm{H}^{+}\right]}{\left[\mathrm{BH}^{+}\right]}$$$$\mathrm{A}^{-}+\mathrm{H}_{2} \mathrm{O} \rightleftharpoons \mathrm{HA}+\mathrm{OH}^{-}$$$$K_{\mathrm{a}} K_{\mathrm{b}}=K_{\mathrm{w}} = 10^{-14}$$$$-\log \left(K_{\mathrm{a}}\right)-\log \left(K_{\mathrm{b}}\right)=-\log \left(K_{\mathrm{w}}\right)$$$$K_{\mathrm{b}}=\frac{[\mathrm{HA}]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{A}^{-}\right]}$$Jump to table of contents.¶
10.¶
Experiment #10 Gibbs Free Energy of a Dissolution Reaction ¶
WHY?¶
This experiment shows how one is able to analyze thermodynamic equations of state in the laboratory. We are able to measure the equilibrium constant K as a function of temperature and pull out thermodynamic values such as $\Delta G°$, $\Delta H°$, $\Delta S°$. Students will standardize HCl (strong acid) and extract thermodynamic variables by varying the reaction temperature for various trials.
Theory¶
We know that Gibbs free energy is central in chemistry and is defined by the following equation:
$$ \Delta G = \Delta H - T\Delta S $$Recall, when the reaction is at equilibrium $\Delta G = 0$, which means that if we want to determine the temperature above equilibrium, then we use the following inequality
$$ 0 > \Delta H - T\Delta S \implies T > \frac{\Delta H}{\Delta S} $$| $$Reactants \rightarrow Products$$ | $$\text{Std Gibbs Free Energy, }\Delta G°$$ | $$\Delta H°$$ | $$T$$ | $$\Delta H°$$ |
|---|---|---|---|---|
| Spontaneous | - | - | $\forall \text{ T}\equiv \text{(For all T)}$ | + |
| Nonspontaneous | + | + | $\forall \text{ T}$ | - |
| Spontaneous | - | - | $T < (\Delta H / \Delta S)$ | - |
| Nonspontaneous | + | + | $T > (\Delta H / \Delta S)$ | + |
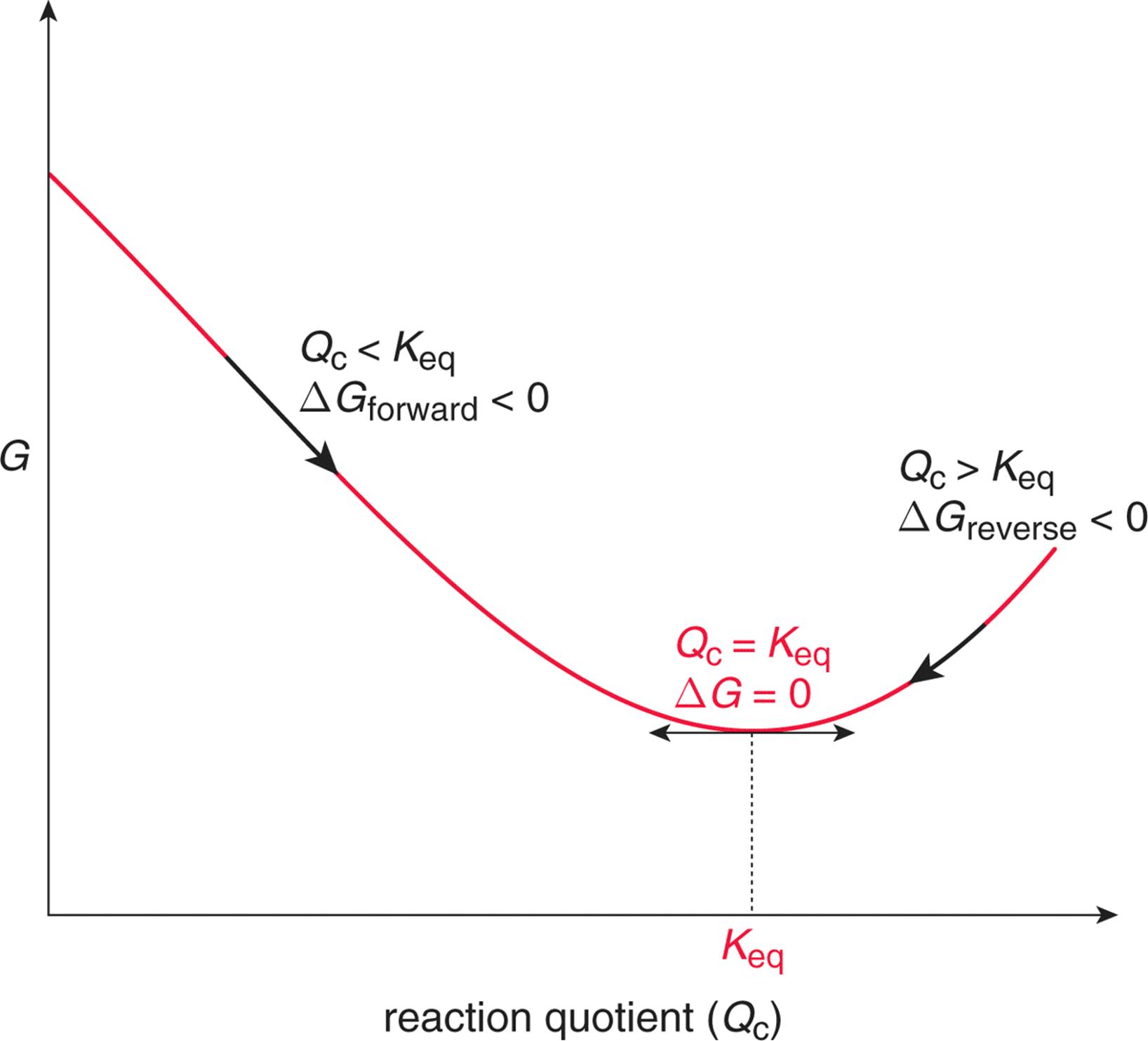
We are looking for an equation that relates thermodynamic state variables with other variables that we can easily measure in the lab, such as temperature and pressure. Here, we will derive an equation that holds temperature constant, but when repeating the reaction over many different temperatures, we can determine $\Delta \mathrm{S}^{\circ}$ and $\Delta \mathrm{H}^{\circ}$.
Again, we say that at equilibrium $\Delta G = 0$ and the reaction quotient, Q goes to $K_{eq}$ , then
$$ \Delta G = \Delta G° + RTlnQ = 0 \implies \Delta \mathrm{G}^{\circ}=-\mathrm{RT} \ln \mathrm{K}_{\mathrm{sp}}$$Now, we substitute $\Delta \mathrm{G}^{\circ}$ into the following equation and rearrange to solve for $\ln K_{\mathrm{sp}}$.
$$\Delta \mathrm{G}^{\circ}=\Delta \mathrm{H}^{\circ}-\mathrm{T} \Delta \mathrm{S}^{\circ}$$$$\ln K_{\mathrm{sp}}=-\frac{\Delta \mathrm{H}^{\circ}}{\mathrm{R}}\left(\frac{1}{\mathrm{T}}\right)+\frac{\Delta \mathrm{S}^{\circ}}{\mathrm{R}}$$Note that this equation represents a straight line:
$$y = m x + b $$What does this plot look like?
Jump to table of contents.¶
11.¶
Experiment #11 Electrochemical Cells ¶
WHY?¶
This experiment
Electrochemistry¶
Electrolysis of $H_{2}O$¶
 Decomposition of pure water into hydrogen and oxygen at standard temperature and pressure is not favorable in thermodynamic terms.
Decomposition of pure water into hydrogen and oxygen at standard temperature and pressure is not favorable in thermodynamic terms.
Cathode (reduction):
$$2 {H^{+}}_{(aq)} + 2e^{−} \rightarrow {H_{2}}_{(g)} \hspace{0.25cm};\hspace{0.25cm} {E°}\text{ = 0.00 V}$$Anode (oxidation):
$$2 {H_{2}O}_{(l)} \rightarrow {O_{2}}_{(g)} + {4H^{+}}_{(aq)} + 4e^{−}\hspace{0.25cm};\hspace{0.25cm} {E°}\text{ = +1.23 V}$$Combining either half reaction pair yields the same overall decomposition of water into oxygen and hydrogen:
Overall reaction:
$$2 {H_{2}O}_{(l)} \rightarrow 2 {H_{2}}_{(g)} + {O_{2}}_{(g)} \hspace{0.25cm};\hspace{0.25cm} {E°}_{cell} = ({E°}_{cathode} − {E°}_{anode}) \text{ = −1.23 V at 25 °C}$$Nernst equation is derived from the standard changes in the Gibbs free energy associated with an electrochemical transformation.
$$\Delta G°= -nFE°, $$where E° is the cell potential and F is the Faraday constant (F = $N_{A}$q, where q is the charge of the electron).
Gibbs free energy and its relation to the cell potential, ${E°}_{cell}$ and the equilibrium constant, K¶
$$\Delta G=\Delta G°+RT lnQ,$$where
$$\Delta G° = -RTlnK$$$$\Delta G = -nF{E}_{cell} \text{ and } \Delta G° = -nF{E°}_{cell}$$then, by substitution we obtain
$Nernst$ equation
$$E=E^{0}-{\frac{RT}{nF}}{ln(Q)} ,$$where F is Faraday's constant and Q is the reaction quotient. Recall that as the system goes to equilibrium as the reaction quotient for the reaction, $Q \rightarrow K_{eq}$ (goes to $K_{eq}$). Temperature, T is in kelvin, Faraday's constant is defined as $F= e N_{A} = 96485.3 C mol^{−1}$, where $N_{A}$ is Avogadro's number and the charge of an electron, $e$ is $1.602×10^{−19} C$. \
Now, suppose we have the following overall chemical reaction:
$$\mathrm{Cu}^{2+}(\mathrm{aq})+\mathrm{Zn}(\mathrm{s}) \rightarrow \mathrm{Cu}(\mathrm{s})+\mathrm{Zn}^{2+}(\mathrm{aq})$$$$ Q = \frac{[\text { Products }]}{[\text { Reactants }]} = \frac{\left[C u(s)\right]\left[{Zn^{2+}}_{(aq)}\right]}{\left[{Cu^{2+}}_{(a q)}\right][Zn_{(s)}]} \\Q= \frac{\left[Z n^{2+}(a q)\right]}{\left[C u^{2+}(a q)\right]} $$$${\displaystyle E=E^{0}-{\frac {2.303RT}{nF}}{\text{pH}}}$$ $$\mathrm{E}_{\text { cell }}=\mathrm{E}_{\text { cell }}^{\mathrm{o}}-\frac{0.0591}{2} \log _{10} \frac{\left[\mathrm{Zn}^{+2}(\mathrm{aq})\right]}{\left[\mathrm{Cu}^{+2}(\mathrm{aq})\right]}$$| $$\text{Std Gibbs Free Energy, }\Delta G°$$ | $${E°}_{cell}$$ | $$K$$ | $$\hspace{1cm}$$ | $$\text{Direction of Reaction}$$ |
|---|---|---|---|---|
| <0 | >0 | $>1$ | $E_{cell}>{E°}_{cell}$ | $\longrightarrow$ |
| >0 | <0 | $<1$ | $E_{cell}<{E°}_{cell}$ | $\longleftarrow$ |
| 0 | 0 | $1$ | $E_{cell}={E°}_{cell}$ | Equilibrium |
Jump to table of contents.¶
12.¶
Final Exam: Written — 60 min ¶
$$\frac{Points}{\text{Total Points}} = 100 /670 \text{ (exam weight > 3 lab reports)}$$¶
• 37 questions - 2.7 pts each
• 7x 1pt bonus questions
What to study:¶
• Pre-lab quizzes
• No electrochemistry
• Mostly nonquantitative, but know important calculations related to the experiment.
Appendix:¶
External Links:
Wolfram Alpha - Computational engine based on a vast collection of built-in data, algorithms and methods - Free version offers limited user interface.
Sympygamma - Similar to Wolfram alpha - Free step-by-step solutions of mathematical operations (requires a numerical pythonic input - easy)
Scale of the Universe - Applet you should check out.