Table of Contents:¶
| Experiment # | Topic |
|---|---|
| 1. | Measurement and Density |
| 2. | Determining Avogadro’s Number |
| 3. | The Empirical Formula of Selected Hydrates |
| 4. | Empirical Formula and Stoichiometry |
| 5. | Reactions and Solubility |
| 6. | Standardization of a base and Titration of a Vinegar Solution |
| 7. | Titration of an Unknown Acid – Determination of Molar Mass |
| 8. | Conductimetric Titrations |
| 9. | Using the Ideal Gas Law |
| 10. | Heats of Reaction and Solution |
| 11. | Solution Preparation and Beers Law |
1.¶
Experiment #1 Measurement and Density¶
This experiment presents us with the historical beauty of Archimedes principle or water displacement (250 BCE).
Vernier Callipers: Learn how to read a Vernier scale JavaScript Applet¶
Jump to table of contents.¶
2.¶
Experiment #2 Determining Avogadro's Number¶
This lab is designed to help students build dimensional analysis skills as well as provide a brief introduction for the organization of molecules at the surface.
Calculations¶
Part A. Determine Avogadro's Number From the Density of Copper¶
Copper crystallizes into a face centered cubic (fcc) unit cell.
The atomic mass of Cu is 63.546 g/mol and the length of one edge in the unit cell is 361.2 pm.
There is 8 corners and 6 faces of the unit cell, where there exists a Cu atom (each of which are shared with other unit cells) at each of these positions.
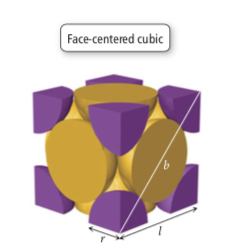
I. Solve for b
$$ b^{2} = l^{2} + l^{2} = 2l^{2} $$
$$ b = \sqrt{2l^{2}} = 4r $$
II. Solve for l
$$ 2l^{2} = b^{2} $$
$$ l = \sqrt{\frac{b^{2}}{2}} = \frac{b}{\sqrt{2}} = \frac{4r}{\sqrt{2}} = 2\sqrt{2}r $$
1. Determine the volume, V of the unit cell.
$$ V_{cube} = l^{3}, \text{ where l is the edge length of the unit cell.} $$
2. Calculate the mass of the unit cell.
$$ Density = \rho = \frac{mass}{volume}$$
$$ Mass_{Cell} = \rho_{Calc}Volume_{Cell}$$
3. Determine the number of atoms that occupy the unit cell.
$$ \text{Atoms/Unit Cell } = (\frac{1}{8}\times \text{# of Corner Atoms}) + (\frac{1}{2} \times \text{# of Face Centered Atoms} )$$
$$ \text{Atoms/Unit Cell } = (\frac{1}{8}\times 8) + (\frac{1}{2} \times 6 ) = 4 $$
4. Use dimensional analysis to calculate Avogadro's number from the number of Cu atoms per unit cell, the mass per unit cell, and the molar mass of Cu.
$$ (\frac{\text{4 Cu Atoms}}{\text{1 Cu Unit Cell}})\times(\frac{\text{1 Cu Unit Cell}}{\text{Mass of Unit Cell}})\times(\frac{63.546 g}{\text{1 mol}}) = \text{# of Cu Atoms} $$
Part B. Stearic Acid Monolayer¶
Check out this video below to see what to look for during the experiment.¶
General idea of what it looks like at the atomic scale:

1. Determine the volume of stearic acid/hexane solution, $V_{SAH}$ using your calibration ratio (drops/mL), $\alpha$ and the average number of drops to form the monolayer.
$$ V_{SAH} = \alpha^{-1}\times(\text{Avg. Drops}) $$
2. Calculate the mass of stearic acid in the monolayer, $m_{stearic}$ using the concentration of stearic acid/hexane solution, $M_{SAH}$.
Note: Molar Mass of Stearic acid is 284.48 g/mol.
$$ m_{stearic} = (M_{SAH})\times(V_{SAH}) $$
3. Calculate the volume of stearic acid in the monolayer, $V_{Stearic}$
$$ V_{Stearic} = (\rho_{Steric Acid})^{-1}\times m_{stearic} $$
$$ $$
4. Calculate the thickness of the monolayer, h where the volume of stearic acid in the monolayer can be approximated by $V=\pi r^{2}h$.
$$ h = \frac{V}{\pi r^{2}} = \frac{V}{\pi(\frac{d}{2})^{2}} $$
5. Determine the volume of a carbon atom.
Note that h/18 can be used as a good approximation for the diameter of a carbon atom.
$$ V_{\text{Carbon atom}} = \frac{4}{3}\pi r^{3} = \frac{4}{3}\pi \frac{d}{2}^{3} = \frac{4}{3}\pi (\frac{h}{36})^{3} $$
6. Determine Avogadro's number.
$$ N_{A} = (\frac{\text{1 Carbon Atom}}{V_{\text{Carbon atom}}})\times(\rho_{\text{Carbon}})^{-1}\times(\frac{\text{12.0107 g Carbon}}{\text{1 mol Carbon}}) $$
Jump to table of contents.¶
5.¶
Experiment #5 Reactions and Solubility¶
Gas forming reactions:
1.
$$2HCl_{(aq)} + K_{2}S \rightarrow H_{2}S (g) + 2KCl (aq)$$2.
$$2HCl_{(aq)} + K_{2}CO_{2} \rightarrow H_{2}O (l) + CO_{2}(g) + 2KCl (aq)$$3.
$$2HCl_{(aq)} + K_{2}SO_{2} \rightarrow H_{2}O (l) + SO_{2}(g) + 2KCl (aq)$$4.
$$NH_{4}Cl(aq) + KOH \rightarrow H_{2}O (l) + NH_{3}(g) + 2KCl (aq)$$5.
$$2HCl_{(aq}) + Zn(s) \rightarrow ZnCl_{2} (aq) + H_{2} (g)$$Weak electrolytes do not dissociate into ions, so another way gases can form in solution is through the decomposition of weak electrolytes. For example, $H_{2}CO_{3}$ readily decomposes into $H_{2}O$ and $CO_{2}$ gas.
Aqueous Solutions; Precipitation Reactions; Acid-base Reactions¶
Use your knowledge of solubility rules: show the net ionic equation, provide the products and balance the chemical equation.¶
(1)
$${SrCl_{2} }_{(aq)} + {H_{2}SO_{4} }_{(aq)} \rightarrow {SrSO_{4}}_{(s)} + {2HCl }_{(aq)}$$$${Sr^{2+} }_{(aq)} + {SO_{4}^{2-}}_{(aq)} \rightarrow {SrSO_{4}}_{(s)}$$$$(H^{+} , Cl^{-} \text{ are spectator ions})$$(2)
$${2 NaOH }_{(aq)} + {H_{2}SO_{4} }_{(aq)} \rightarrow {Na_{2}SO_{4}}_{(aq)} + {2H_{2}O }_{(l)}$$$$2H^{+} + 2OH^{-} \rightarrow {2H_{2}O }_{(l)}$$$$(Na^{+} , SO_{4}^{2-} \text{ are spectator ions})$$(3)
$${(NH_{4})_{2}SO_{4} }_{(aq)} + {2NaOH}_{(aq)} \rightarrow {Na_{2}SO_{4} }_{(aq)} + {2NH_{3}}_{(g)} + {2H_{2}O }_{(l)}$$$${2NH_{4}^{+} }_{(aq)} + {2OH^{-} }_{(aq)} \rightarrow {2NH_{3}}_{(g)} + {2H_{2}O }_{(l)}$$$$(Na^{+} , SO_{4}^{2-} \text{ are spectator ions})$$(4) Balance the following equations and then write the net ionic equations.
(a)
$$(NH_{4})_{2}CO_{3}(aq) + Cu(NO_{3})_{2}(aq) \rightarrow CuCO_{3}(s) + NH_{4}NO_{3}(aq)$$Answer:
Balanced Eq:
$$(NH_{4})_{2}CO_{3}(aq)+ Cu(NO_{3})_{2}(aq) \rightarrow CuCO_{3}(s) + 2 NH_{4}NO_{3}(aq)$$Net:
$$Cu^{2+}(aq)+ CO_{3}^{2-}(aq) \rightarrow CuCO_{3} (s)$$(b)
$$Pb(OH)_{2}(s) + HCl(aq) \rightarrow PbCl_{2}(s) + H_{2}O(l)$$Answer:
Balanced Eq:
$$Pb(OH)_{2}(s) + 2 HCl(aq) \rightarrow PbCl_{2}(s) + 2 H_{2}O(l)$$Net:
$$Pb(OH)_{2}(s) + 2 H^{+}(aq)+ 2 Cl^{-}(aq) \rightarrow PbCl_{2}(s) + 2 H_{2}O(l)$$(c)
$$BaCO_{3}(s) + HCl(aq) \rightarrow BaCl_{2}(aq)+ H_{2}O(l) + CO_{2}(g)$$Answer: Balanced Eq:
$$BaCO_{3}(s) + 2 HCl(aq) \rightarrow BaCl_{2}(aq) + H_{2}O(l) + CO_{2}(g)$$Net:
$$BaCO_{3}(s) + 2H^{+}(aq) \rightarrow Ba^{2+}(aq) + H_{2}O(l) + CO_{2}(g)$$(d)
$$CH_{3}CO_{2}H(aq) + Ni(OH)_{2}(s) \rightarrow Ni(CH_{3}CO_{2})_{2}(aq) + H_{2}O(l)$$Answer:
Balanced Eq:
$$2 CH_{3}CO_{2}H(aq) + Ni(OH)_{2}(s) \rightarrow Ni(CH_{3}CO_{2})_{2}(aq) + 2 H_{2}O(l)$$Net:
$$2CH_{3}CO_{2}H(aq) + Ni(OH)_{2}(s) \rightarrow 2 CH_{3}CO_{2}^{-} (aq) + Ni^{2+}(aq) + 2H_{2}O(l)$$Jump to table of contents.¶
6.¶
Experiment #6 Standardization of a base and Titration of a Vinegar Solution¶
Jump to table of contents.¶
7.¶
Experiment #7 Titration of an Unknown Acid – Determination of Molar Mass¶
Jump to table of contents.¶
8.¶
Experiment #8 Conductimetric Titrations¶
This lab is continuation of the various application of titrations.
Where is conductivity found in environmental applications?
• Water treatment
• Aquacultures
• Irrigation/ Agriculture
Theory - a very brief Introduction to Electrochemistry¶
Ohm's Law: $V = IR$
V = Potential difference in voltz, V
I = Current in Amphere's, A
R = Resistance in ohms, $\Omega$
Conductance, G is the reciprocal of resistance and is measured in siemens(S). German inventor Werner Von Siemens (mid 1800's)
$$G \frac{1}{R} = \frac{\kappa A}{l} $$A = Area of electrode ($m^{2}$)
l = distance between electrodes (m)
Conductivity, $\kappa$ ($Sm^{-1}$) is then defined as $\kappa = \frac{l}{RA} $, where $\frac{l}{A}$ is typically called the cell constant, $c^{*}$.
Side Notes:
Although conductivity, $\kappa$ is not in terms of temperature in the equation above. Generally, ionic conductivity increases with increasing temperature. As the mobility of ions increase with temperature, so will conductivity.
Jump to table of contents.¶
11.¶
Experiment #11 Solution Preparation and Beers Law¶
This lab was designed to help students develop the skills for determining the amount of a certain species inside some solution by linear regression, where the equation of a line is given by Beer's Law.
Theory:¶

Derivation of Beer's Law:¶
Here is an image of the situation we wish to model:

The density of particles, $\rho$ and the absorption coefficient, $\alpha$ multiplied by the intensity, I shown in the 1st order differential equation: $$ -\frac{\partial{I}}{\partial{x}} = I \alpha \rho $$
Combine like-terms to each side of the equation:
$$\int_{I_{0}}^{I} \frac{\partial{I}}{I} = -\int_{0}^{x} \alpha \rho \partial{x} $$We know that $\int \frac{1}{x}dx = ln(x)$, so
$$ln(\frac{I}{I_{0}}) = - \alpha \rho x, $$To get the general solution of the D.E we can take the exponential of both sides
$$\frac{I}{I_{0}} = e^{-\alpha \rho x} $$General Solution to the D.E:
$$I (x) = I_{0} e^{-\alpha \rho x}$$Otherwise, to continue deriving Beer's Law we can use the property of logarithms:
$$-ln(\frac{I}{I_{0}}) = ln(\frac{I_{0}}{I}) = \alpha \rho x, $$and since we know the following
$$log_{10}(x) = \frac{ln(x)}{ln(10)},$$then we can say
$$ log_{10}(\frac{I_{0}}{I}) = \frac{\alpha \rho x}{ln(10)}$$Finally, we can say that $\rho \propto c$. We can also simplify further by saying $\epsilon =\frac{\alpha}{ln(10)}$, which has units of $M^{-1}cm^{-1}$ and $x = b$, where b is in cm.
$$ A = ln(\frac{I_{0}}{I}) = \epsilon b c$$Theory - a brief Introduction to Quantum Mechanics - particle in a box (PIB)¶
$$\Delta E = E_{S_{1}} − E_{S_{0}}$$$$E_{n} =\frac{h^{2}n^{2}}{8ma^{2}}$$$$ \Delta E = \frac{h^{2}(N+1)^{2}}{8ma^{2}} = h\nu = \lambda $$n = 1, 2, 3..., h = 6.62608 × 10-34 J·s (Planck’s constant), m = 9.10939 × 10-31 kg (mass of an electron), and a = length of the box (in meters if using SI units).
Solving for the box length, a, gives:
$$a = \sqrt{\frac{h\lambda (N+1)}{8mc} } $$The box length, a, may also be related to the polyene structure with the empirical formula:
$$a = (P · l) + E$$where $P$ is the number of C atoms in the conjugated chain, $l$ is the C-C bond length in the chain, and $E$ is the effective size of the end-groups.
Where & how can this be applied?¶
$\beta$-carotin is the chemical that gives carrots their characteristic orange color. Absorbance is around 450 nm (violet-blue), so we see orange, which is the light transmitted.
Color Wheel with corresponding wavelengths:¶

Jump to table of contents.¶
Appendix:¶
Some of the Main Types of Reactions:¶
1) Combination (synthesis)¶
$$ \mathrm{A}+\mathrm{B} \rightarrow \mathrm{C} $$$$ {2H_{2}}_{(g)} + {O_{2}}_{(g)} \rightarrow {2H_{2}O}_{(g)}\tag{1} $$2) Decomposition¶
$$ \mathrm{C} \rightarrow \mathrm{A}+\mathrm{B} $$$$ {2H_{2}O}_{(g)} \rightarrow {2H_{2}}_{(g)} + {O_{2}}_{(g)} \tag{1}$$3) Single Displacement¶
$$ \mathrm{AB}+\mathrm{C} \rightarrow \mathrm{CB}+\mathrm{A} $$$${{CuSO}_{4}}_{(aq)} + Zn_{(s)} \rightarrow {Zn{SO}_{4}}_{(aq)}+Cu_{(s)}\tag{1}$$4) Double Displacement¶
$$ \mathrm{AB}+\mathrm{CD} \rightarrow \mathrm{AD}+\mathrm{BC} $$$$ \mathrm{AgNO}_{3}+\mathrm{NaCl} \rightarrow \mathrm{AgCl}+\mathrm{NaNO}_{3}\tag{1}$$$$ {NaHCO_{3}}_{(aq)} + {CH_{3}COOH}_{(aq)} \rightarrow {H_{2}CO_{3}}_{(aq)} + {NaCH_{3}COO}_{(s)} \rightarrow {H_{2}O}_{(l)} + {CO_{2}}_{(g)} + {NaCH_{3}COO}_{(s)}\tag{2}$$5) Neutralization¶
Double displacement reactions between strong acids and strong bases results in salt and water:
$$\mathrm{HCl}_{(aq)}+\mathrm{NaOH}_{(aq)} \rightarrow \mathrm{NaCl}_{(aq)}+\mathrm{H}_{2} \mathrm{O}_{(l)}\tag{1}$$Double displacement reactions between acids and bases (water as solvent) results in salt :
$${NaHCO_{3}}_{(aq)} + {CH_{3}COOH}_{(aq)} \rightarrow {H_{2}CO_{3}}_{(aq)} + {NaCH_{3}COO}_{(s)}\tag{2}$$6) Combustion¶
These reactions always result in a change in enthalpy, $\Delta H_{combust} < 0$ and forms $CO_{2}$ and $H_{2}O$.
$$CH_{4} + 2O_{2} \rightleftharpoons CO_{2} + 2H_{2}O\hspace{0.2cm};\hspace{0.2cm} \Delta H < 0 \tag{1}$$Suppose wood has the chemical formula $\mathbf{C}_{6} \mathbf{H}_{12} \mathbf{O}_{6}$. Then,
$$\mathbf{C}_{6} \mathbf{H}_{12} \mathbf{O}_{6} \quad+6 \mathbf{O}_{2}\rightleftharpoons\quad 6 \mathrm{CO}_{2} \quad+\quad 6 \mathbf{H}_{2} \mathbf{O}\hspace{0.2cm};\hspace{0.2cm} \Delta H <0 \tag{2}$$7) Redox¶
$${{CuSO}_{4}}_{(aq)} + Zn_{(s)} \rightarrow {Zn{SO}_{4}}_{(aq)}+Cu_{(s)}\tag{1}$$Jump to table of contents.¶
External Links:
Wolfram Alpha - Computational engine based on a vast collection of built-in data, algorithms and methods - Free version offers limited user interface.
Sympygamma - Similar to Wolfram alpha - Free step-by-step solutions of mathematical operations (requires a numerical pythonic input - easy)
Scale of the Universe - Applet you should check out.